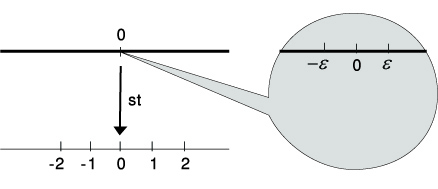

What's new with infinitesimals? Provided below are
links to over 80 recent publications on
infinitesimals and related subjects by
Jacques Bair,
Tiziana Bascelli,
Piotr Błaszczyk,
Alexandre
Borovik,
Emanuele Bottazzi,
Robert Ely,
Peter
Fletcher,
Elías Fuentes Guillén,
Peter Heinig,
Valérie Henry,
Frederik
Herzberg,
Karel Hrbacek,
Renling Jin,
Vladimir Kanovei,
Boris
Katz,
Karin Katz,
Taras Kudryk,
Karl Kuhlemann,
Semen Samsonovich Kutateladze,
Eric Leichtnam,
Claude Lobry,
Thomas McGaffey,
Thomas Mormann,
Tahl Nowik,
Luie
Polev,
Patrick Reeder,
Sam Sanders,
Jan
Peter Schäfermeyer,
David Sherry,
David Tall,
Monica Ugaglia,
Mark
van Atten,
and others.
A nice introduction to our program can be found in the
MathSciNet review by M. Guillaume in pdf
To see where the papers have appeared click on List of periodicals
See List of critics and
Reception
See Reappraisal of the
procedures of the pioneers of infinitesimal analysis
See Alphabetical list of vignettes
on various topics related to infinitesimals
year '26 (2 publications)
26b. Katz, M.; Kuhlemann, K.; Kutateladze, S. "Marx versus Engels on infinitesimals: Chimera or triumph?" HOPOS (History of Philosophy of Science) 16 (2026), no. 1. https://doi.org/10.1086/739306. See also Marx versus Engels
26c. Katz, M.; Kuhlemann, K.; Sanders, S.; Sherry, D. "Formalism 25." Journal for General Philosophy of Science (2026). https://doi.org/10.1007/s10838-025-09726-8, https://arxiv.org/pdf/2502.14811
year '25 (2 publications)
25a. Katz, M. "Episodes from the history of infinitesimals." British Journal for the History of Mathematics 40 (2025), no. 2, 123-135. https://doi.org/10.1080/26375451.2025.2474811, https://arxiv.org/abs/2503.04313, https://mathscinet.ams.org/mathscinet/article?mr=4960088
25b. Kuhlemann, K. Nonstandard analysis: In Higher Education, Logic and Philosophy. de Gruyter, Berlin/Boston, 2025. https://doi.org/10.1515/9783111429687, Google Book
'20-'24 (27 publications)
year '24 (5 publications)
24a. Bottazzi, E.; Katz, M. "History of Archimedean and non-Archimedean approaches to uniform processes: Uniformity, symmetry, regularity." Antiquitates Mathematicae 18 (2024), 105-148. https://dx.doi.org/10.14708/am.v18i1.7332, https://arxiv.org/abs/2502.18319, https://mathscinet.ams.org/mathscinet/article?mr=4876646 see also Non-Archimedean probability
24b. Hrbacek, K. "Multi-level nonstandard analysis and the Axiom of Choice." Journal of Logic and Analysis 16:5 (2024), 1-29. https://doi.org/10.4115/jla.2024.16.5, https://arxiv.org/abs/2405.00621, https://mathscinet.ams.org/mathscinet/article?mr=4772843
24c. Katz, M.; Kuhlemann, K.; Sherry, D. "A Leibniz/NSA comparison." London Mathematical Society Newsletter (2024), no. 512, 33-37. https://www.lms.ac.uk/sites/default/files/inline-files/NLMS_512%20Online_0.pdf , http://arxiv.org/abs/2409.17154. See also Leibniz/NSA comparison video
24d. Katz, M.; Kuhlemann, K.; Sherry, D.; Ugaglia, M. "Leibniz on bodies and infinities: rerum natura and mathematical fictions." Review of Symbolic Logic 17 (2024), no. 1, 36-66. https://doi.org/10.1017/S1755020321000575, https://arxiv.org/abs/2112.08155,
24e. Ugaglia, M.; Katz, M. "Evolution of Leibniz’s thought in the matter of fictions and infinitesimals." In: Sriraman, B. (ed.) Handbook of the History and Philosophy of Mathematical Practice, pp. 341-384, Springer, Cham, 2024. https://doi.org/10.1007/978-3-030-19071-2_149-1, https://arxiv.org/abs/2310.14249, https://mathscinet.ams.org/mathscinet/article?mr=4786387
year '23 (8 publications)
23a. Bair, J.; Borovik, A.; Kanovei, V.; Katz, M.; Kutateladze, S.; Sanders, S.; Sherry, D.; Ugaglia, M.; van Atten, M. "Is pluralism in the history of mathematics possible?" The Mathematical Intelligencer 45 (2023), no. 1, 8. https://doi.org/10.1007/s00283-022-10248-0, https://arxiv.org/abs/2212.12422, https://mathscinet.ams.org/mathscinet-getitem?mr=4559464. See also Depictions.
23b. Heinig, P.; Katz, M.; Kuhlemann, K.; Schaefermeyer, J.P.; Sherry, D. "Exploring Felix Klein's contested modernism." Antiquitates Mathematicae 17 (2023), 101-137. https://dx.doi.org/10.14708/am.v17i1.7245, https://arxiv.org/abs/2402.00122, https://mathscinet.ams.org/mathscinet/article?mr=4706521
23c. Hrbacek, K.; Katz, M. "Constructing nonstandard hulls and Loeb measures in internal set theories." Bulletin of Symbolic Logic 29 (2023), no. 1, 97-127. https://doi.org/10.1017/bsl.2022.43, https://arxiv.org/abs/2301.00367, https://mathscinet.ams.org/mathscinet-getitem?mr=4560535
23d. Hrbacek, K.; Katz, M. "Effective infinitesimals in ℝ." Real Analysis Exchange 48 (2023), no. 2, 365-380. https://arxiv.org/abs/2305.09672, https://doi.org/10.14321/realanalexch.48.2.1671048854, https://mathscinet.ams.org/mathscinet/article?mr=4668954
23e. Hrbacek, K.; Katz, M. "Peano and Osgood theorems via effective infinitesimals." Journal of Logic and Analysis 15:6 (2023), 1-19. https://doi.org/10.4115/jla.2023.15.6, https://arxiv.org/abs/2311.01374, https://mathscinet.ams.org/mathscinet/article?mr=4673816
23f. Katz, M.; Kuhlemann, K. "Leibniz's contested infinitesimals: Further depictions." Gaṇita Bhāratī 45 (2023), no. 1, 77-112. https://doi.org/10.32381/GB.2023.45.1.4, https://arxiv.org/abs/2501.01193 See also Depictions.
23g. Katz, M.; Sherry, D.; Ugaglia, M. "Of pashas, popes, and indivisibles." Science in Context 36 (2023), no. 2, 123-146. https://doi.org/10.1017/S0269889725000456, https://arxiv.org/abs/2502.11145, https://mathscinet.ams.org/mathscinet/article?mr=4954137
23h. Katz, M.; Sherry, D.; Ugaglia, M. "When does a hyperbola meet its asymptote? Bounded infinities, fictions, and contradictions in Leibniz." Revista Latinoamericana de Filosofía 49 (2023), no. 2, 241-258. https://doi.org/10.36446/rlf2023359, https://arxiv.org/abs/2311.06023
22a. Bair, J.; Borovik, A.; Kanovei, V.; Katz, M.; Kutateladze, S.; Sanders, S.; Sherry, D.; Ugaglia, M. "Historical infinitesimalists and modern historiography of infinitesimals." Antiquitates Mathematicae 16 (2022), 189-257. https://doi.org/10.14708/am.v16i1.7169, https://arxiv.org/abs/2210.14504, https://mathscinet.ams.org/mathscinet-getitem?mr=4570174
22b. Katz, M.; Kuhlemann, K.; Sherry, D.; Ugaglia, M.; van Atten, M. "Two-track depictions of Leibniz's fictions." The Mathematical Intelligencer 44 (2022), no. 3, 261-266. https://doi.org/10.1007/s00283-021-10140-3, https://arxiv.org/abs/2111.00922, https://mathscinet.ams.org/mathscinet-getitem?mr=4480193. See also Depictions.
year '21 (7 publications)
21a. Bair, J.; Błaszczyk, P.; Ely, R.; Katz, M.; Kuhlemann, K. "Procedures of Leibnizian infinitesimal calculus: An account in three modern frameworks." British Journal for the History of Mathematics 36 (2021), no. 3, 170-209. https://doi.org/10.1080/26375451.2020.1851120, https://arxiv.org/abs/2011.12628, https://mathscinet.ams.org/mathscinet-getitem?mr=4353153, cited by over 20 articles:
21b. Bottazzi, E; Katz, M. "Infinite lotteries, spinners, and the applicability of hyperreals." Philosophia Mathematica 29 (2021), no. 1, 88-109. https://doi.org/10.1093/philmat/nkaa032, https://arxiv.org/abs/2008.11509, https://mathscinet.ams.org/mathscinet-getitem?mr=4267988
21c. Bottazzi, E; Katz, M. "Internality, transfer, and infinitesimal modeling of infinite processes." Philosophia Mathematica 29 (2021), no. 2, 256-277. https://doi.org/10.1093/philmat/nkaa033, https://arxiv.org/abs/2008.11513, https://mathscinet.ams.org/mathscinet-getitem?mr=4492449
21d. Bottazzi, E; Katz, M. "Infinitesimals via Cauchy sequences: Refining the classical equivalence." Open Mathematics 19 (2021), 477-482. https://doi.org/10.1515/math-2021-0048, https://arxiv.org/abs/2106.00229, https://mathscinet.ams.org/mathscinet-getitem?mr=4267478. The article includes an analysis of Peano's little-known contribution to a theory of infinitesimals.
21e. Hrbacek, K.; Katz, M. "Infinitesimal analysis without the Axiom of Choice." Annals of Pure and Applied Logic 172 (2021), no. 6, 102959. https://doi.org/10.1016/j.apal.2021.102959, https://arxiv.org/abs/2009.04980, https://mathscinet.ams.org/mathscinet-getitem?mr=4224071. See also Introduction to infinitesimal analysis without the axiom of choice, cited by ~20 articles:
21f. Katz, M. "A two-track tour of Cauchy's Cours." Mathematics Today 57 (2021), no. 4, 154-158. Reprint in pdf, https://arxiv.org/abs/2107.00207, https://mathscinet.ams.org/mathscinet-getitem?mr=4401322
21g. Katz, M.; Kuhlemann, K.; Sherry, D.; Ugaglia, M. "Three case studies in current Leibniz scholarship." Antiquitates Mathematicae 15 (2021), 147-168. https://dx.doi.org/10.14708/am.v15i1.7087, https://arxiv.org/abs/2201.02047, https://mathscinet.ams.org/mathscinet-getitem?mr=4467506
year '20 (5 publications)
20a. Bair, J.; Błaszczyk, P.; Fuentes Guillén, E.; Heinig, P.; Kanovei, V.; Katz, M. "Continuity between Cauchy and Bolzano: Issues of antecedents and priority." British Journal for the History of Mathematics 35 (2020), no. 3, 207-224. https://doi.org/10.1080/26375451.2020.1770015, https://arxiv.org/abs/2005.13259, https://mathscinet.ams.org/mathscinet-getitem?mr=4154872, cited by:
20b. Bair, J.; Błaszczyk, P.; Heinig, P.; Kanovei, V.; Katz, M. "Cauchy's work on integral geometry, centers of curvature, and other applications of infinitesimals." Real Analysis Exchange 45 (2020), no. 1, 127-150. reprint, https://arxiv.org/abs/2003.00438, https://mathscinet.ams.org/mathscinet-getitem?mr=4196072
20c. Ely, R. "Teaching calculus with infinitesimals and differentials." ZDM 53 (2021), 591-604. https://doi.org/10.1007/s11858-020-01194-2
20d. Kanovei, V.; Katz, M.; Nowik, T. "Metric completions, the Heine-Borel property, and approachability." Open Mathematics 18 (2020), 162-166. https://doi.org/10.1515/math-2020-0017, https://arxiv.org/abs/2002.07536, https://mathscinet.ams.org/mathscinet-getitem?mr=4080273
20e. Katz, M. "Mathematical conquerors, Unguru polarity, and the task of history." Journal of Humanistic Mathematics 10 (2020), no. 1, 475-515. https://doi.org/10.5642/jhummath.202001.27, https://arxiv.org/abs/2002.00249, https://mathscinet.ams.org/mathscinet-getitem?mr=4060619, cited by:
'15-'19 (32 publications)
year '19 (4 publications)
19a. Bair, J.; Błaszczyk, P.; Heinig, P.; Kanovei, V.; Katz, M. "19th century real analysis, forward and backward." Antiquitates Mathematicae 13 (2019), 19-49. https://doi.org/10.14708/am.v13i1.6440, https://arxiv.org/abs/1907.07451, https://mathscinet.ams.org/mathscinet-getitem?mr=4075256
19b. Bascelli, T.; Błaszczyk, P.; Kanovei, V.; Katz, K.; Katz, M.; Kutateladze, S.; Nowik, T.; Schaps, D.; Sherry, D. "Gregory's sixth operation." In The Best Writing on Mathematics 2019, 195-207. Edited by Mircea Pitici. Princeton University Press, Princeton, NJ, 2019. https://books.google.co.il/books?id=RcmXDwAAQBAJ, https://mathscinet.ams.org/mathscinet-getitem?mr=4528717
19c. Bottazzi, E. "Homomorphisms between rings with infinitesimals and infinitesimal comparisons." Mat. Stud. 52 (2019), no. 1, 3-9. https://doi.org/10.30970/ms.52.1.3-9, https://arxiv.org/abs/1902.06076
19d. Bottazzi, E.; Kanovei, V.; Katz, M.; Mormann, T.; Sherry, D. "On mathematical realism and the applicability of hyperreals." Mat. Stud. 51 (2019), no. 2, 200-224. https://doi.org/10.15330/ms.51.2.200-224, https://arxiv.org/abs/1907.07040, https://mathscinet.ams.org/mathscinet-getitem?mr=3988243, cited by:
year '18 (12 publications)
18a. Bair, J.; Błaszczyk, P.; Ely, R.; Heinig, P.; Katz, M. "Leibniz's well-founded fictions and their interpretations." Mat. Stud. 49 (2018), no. 2, 186-224. https://doi.org/10.15330/ms.49.2.186-224, https://arxiv.org/abs/1812.00226, https://mathscinet.ams.org/mathscinet-getitem?mr=3882551, cited by over 20 articles:
18b. Bair, J.; Błaszczyk, P.; Heinig, P.; Katz, M.; Schäfermeyer, J.; Sherry, D. "Klein vs Mehrtens: restoring the reputation of a great modern." Mat. Stud. 48 (2017), no. 2, 189-219. https://arxiv.org/abs/1803.02193, https://doi.org/10.15330/ms.48.2.189-219 , https://mathscinet.ams.org/mathscinet-getitem?mr=3819950
18c. Bair, J.; Błaszczyk, P.; Katz, K.; Katz, M.; Kudryk, T.; Sherry, D. "Analyzing Benardete's comment on decimal notation." Philosophy of Mathematics Education Journal no. 33, january 2018. at journal and https://arxiv.org/abs/1706.00191
18d. Bair, J.; Katz, M.; Sherry, D. "Fermat's dilemma: Why did he keep mum on infinitesimals? and the European theological context." Foundations of Science 23 (2018), no. 3, 559-595.
18e. Bascelli, T.; Błaszczyk, P.; Borovik, A.; Kanovei, V.; Katz, K.; Katz, M.; Kutateladze, S.; McGaffey, T.; Schaps, D.; Sherry, D. "Cauchy's infinitesimals, his sum theorem, and foundational paradigms." Foundations of Science 23 (2018), no. 2, 267-296. https://doi.org/10.1007/s10699-017-9534-y, https://arxiv.org/abs/1704.07723, https://mathscinet.ams.org/mathscinet-getitem?mr=3803893, cited by over 20 articles:
18f. Bascelli, T.; Błaszczyk, P.; Kanovei, V.; Katz, K.; Katz, M.; Kutateladze, S.; Nowik, T.; Schaps, D.; Sherry, D. "Gregory's sixth operation." Foundations of Science 23 (2018), no. 1, 133-144. https://doi.org/10.1007/s10699-016-9512-9, https://arxiv.org/abs/1612.05944, https://mathscinet.ams.org/mathscinet-getitem?mr=3772065
18g. Błaszczyk, P.; Kanovei, V.; Katz, M.; Nowik, T. "Monotone subsequence via ultrapower." Open Mathematics 16 (2018), 149-153. https://doi.org/10.1515/math-2018-0015, https://arxiv.org/abs/1803.00312, https://mathscinet.ams.org/mathscinet-getitem?mr=3772690
18h. Herzberg, F.; Kanovei, V.; Katz, M.; Lyubetsky, V. "Minimal axiomatic frameworks for definable hyperreals with transfer." Journal of Symbolic Logic 83 Issue 1, march 2018, pp. 385-391. https://doi.org/10.1017/jsl.2017.48, https://arxiv.org/abs/1707.00202, https://mathscinet.ams.org/mathscinet-getitem?mr=3796290
18i. Kanovei, V.; Katz, K.; Katz, M.; Mormann, T. "What makes a theory of infinitesimals useful? A view by Klein and Fraenkel." Journal of Humanistic Mathematics 8 (2018), no. 1, 108-119. https://scholarship.claremont.edu/jhm/vol8/iss1/7, https://arxiv.org/abs/1802.01972, https://mathscinet.ams.org/mathscinet-getitem?mr=3762866
18j. Katz, B.; Katz, M; Sanders, S. "A footnote to The crisis in contemporary mathematics." Historia Mathematica 45 (2018), no. 2, 176-181. https://doi.org/10.1016/j.hm.2018.03.002, https://arxiv.org/abs/1804.02645 , https://mathscinet.ams.org/mathscinet-getitem?mr=3802555 A portrait of Errett Bishop as a young... chicken.
18k. Sherry, D. "The jesuits and the method of indivisibles." Foundations of Science 23 (2018), no. 2, 367-392. https://doi.org/10.1007/s10699-017-9525-z, https://mathscinet.ams.org/mathscinet-getitem?mr=3803897
18l. Sanders, S. "To be or not to be constructive, that is not the question." Indag. Math. (N.S.) 29 (2018), no. 1, 313-381. https://doi.org/10.1016/j.indag.2017.05.005, https://mathscinet.ams.org/mathscinet-getitem?mr=3739620
year '17 (9 publications)
17a. Bair, J.; Błaszczyk, P.; Ely, R.; Henry, V.; Kanovei, V.; Katz, K.; Katz, M.; Kudryk, T.; Kutateladze, S.; McGaffey, T.; Mormann, T.; Schaps, D.; Sherry, D. "Cauchy, infinitesimals and ghosts of departed quantifiers." Mat. Stud. 47 (2017), no. 2, 115-144.
17b. Bair, J.; Błaszczyk, P.; Ely, R.; Henry, V.; Kanovei, V.; Katz, K.; Katz, M.; Kutateladze, S.; McGaffey, T.; Reeder, P.; Schaps, D.; Sherry, D.; Shnider, S. "Interpreting the infinitesimal mathematics of Leibniz and Euler." Journal for General Philosophy of Science 48 (2017), no. 2, 195-238. https://doi.org/10.1007/s10838-016-9334-z and https://arxiv.org/abs/1605.00455 and https://www.ams.org/mathscinet-getitem?mr=3663035 Here we analyze Euler's approach to infinitesimal analysis and his proof of the infinite product decomposition for the sine function. We also examine Giovanni Ferraro's flawed historical scholarship and propose a sounder alternative. Cited by over 40 articles:
17c. Błaszczyk, P.; Kanovei, V.; Katz, K.; Katz, M.; Kudryk, T.; Mormann, T.; Sherry, D. "Is Leibnizian calculus embeddable in first order logic?" Foundations of Science 22 (2017), no. 4, 717-731. https://doi.org/10.1007/s10699-016-9495-6 and https://arxiv.org/abs/1605.03501 and https://mathscinet.ams.org/mathscinet-getitem?mr=3720412
17d. Błaszczyk, P.; Kanovei, V.; Katz, K.; Katz, M.; Kutateladze, S.; Sherry, D. "Toward a history of mathematics focused on procedures." Foundations of Science 22 (2017), no. 4, 763-783. https://doi.org/10.1007/s10699-016-9498-3, https://arxiv.org/abs/1609.04531, https://mathscinet.ams.org/mathscinet-getitem?mr=3720415 Here we propose an approach to the history of mathematics that focuses on the procedures of the historical masters rather than set-theoretic ontology of the entities they use. We also examine Jeremy Gray's flawed historical scholarship and propose a sounder alternative.
17e. Błaszczyk, P.; Kanovei, V.; Katz, M.; Sherry, D. "Controversies in the foundations of analysis: Comments on Schubring's Conflicts." Foundations of Science 22 (2017), no. 1, 125-140. https://doi.org/10.1007/s10699-015-9473-4, https://arxiv.org/abs/1601.00059, https://www.ams.org/mathscinet-getitem?mr=3605125 See also Reception
17f. Fletcher, P.; Hrbacek, K.; Kanovei, V.; Katz, M.; Lobry, C.; Sanders, S. "Approaches to analysis with infinitesimals following Robinson, Nelson, and others." Real Analysis Exchange 42 (2017), no. 2, 193-252. reprint, https://doi.org/10.14321/realanalexch.42.2.0193, https://arxiv.org/abs/1703.00425, https://mathscinet.ams.org/mathscinet-getitem?mr=3721800, cited by over 40 articles:
17g. Gutman, A.; Katz, M.; Kudryk, T.; Kutateladze, S. "The Mathematical Intelligencer flunks the Olympics." Foundations of Science 22 (2017), no. 3, 539-555. https://doi.org/10.1007/s10699-016-9485-8, https://arxiv.org/abs/1606.00160, https://www.ams.org/mathscinet-getitem?mr=3696393 Here we examine Yaroslav Sergeyev's grossbit pathos.
17h. Katz, M.; Polev, L. "From Pythagoreans and Weierstrassians to true infinitesimal calculus." Journal of Humanistic Mathematics 7 (2017), no. 1, 87-104. https://doi.org/10.5642/jhummath.201701.07, https://arxiv.org/abs/1701.05187 cited by 20 articles:
17i. Sanders, S. "Reverse Formalism 16." Synthese 197 (2020), no. 2, 497-544. https://doi.org/10.1007/s11229-017-1322-2, https://arxiv.org/abs/1701.05066, https://mathscinet.ams.org/mathscinet-getitem?mr=4072261
year '16 (3 publications)
16a. Bascelli, T.; Błaszczyk, P.; Kanovei, V.; Katz, K.; Katz, M.; Schaps, D.; Sherry, D. "Leibniz versus Ishiguro: Closing a Quarter Century of Syncategoremania." HOPOS: The Journal of the International Society for the History of Philosophy of Science 6 (2016), no. 1, 117-147. https://doi.org/10.1086/685645, https://arxiv.org/abs/1603.07209
16b. Błaszczyk, P.; Borovik, A.; Kanovei, V.; Katz, M.; Kudryk, T.; Kutateladze, S.; Sherry, D. "A non-standard analysis of a cultural icon: The case of Paul Halmos." Logica Universalis 10 (2016), no. 4, 393-405. https://doi.org/10.1007/s11787-016-0153-0, https://arxiv.org/abs/1607.00149, https://www.ams.org/mathscinet-getitem?mr=3566230
16c. Kanovei, V.; Katz, K.; Katz, M.; Nowik, T. "Small oscillations of the pendulum, Euler's method, and adequality." Quantum Studies: Mathematics and Foundations 3 (2016), no. 3, 231-236. https://doi.org/10.1007/s40509-016-0074-x and https://arxiv.org/abs/1604.06663 and https://www.ams.org/mathscinet-getitem?mr=3531864
year '15 (4 publications)
15a. Kanovei, V.; Katz, K.; Katz, M.; Schaps, M. "Proofs and Retributions, Or: Why Sarah Can't Take Limits." Foundations of Science 20 (2015), no. 1, 1-25. https://doi.org/10.1007/s10699-013-9340-0, https://www.ams.org/mathscinet-getitem?mr=3312498 Here we examine Errett Bishop's criticisms of Robinson's framework. We also compare Bishop's attitude with Heyting's.
15b. Kanovei, V.; Katz, K.; Katz, M.; Sherry, D. "Euler's lute and Edwards' oud." The Mathematical Intelligencer 37 (2015), no. 4, 48-51. https://doi.org/10.1007/s00283-015-9565-6, https://arxiv.org/abs/1506.02586, https://www.ams.org/mathscinet-getitem?mr=3435825 see also Reception
15c. Katz, M.; Kutateladze, S. "Edward Nelson (1932-2014)." The Review of Symbolic Logic 8 (2015), no. 3, 607-610. https://doi.org/10.1017/S1755020315000015, https://arxiv.org/abs/1506.01570
15d. Nowik, T; Katz, M. "Differential geometry via infinitesimal displacements." Journal of Logic and Analysis 7:5 (2015), 1-44. https://www.logicandanalysis.com/index.php/jla/article/view/237, https://u.math.biu.ac.il/~katzmik/dgnsa_arxiv.pdf, https://arxiv.org/abs/1405.0984, https://www.ams.org/mathscinet-getitem?mr=3457545
'10-'14 (23 publications)
year '14 (4 publications)
14a. Bascelli, T.; Bottazzi, E.; Herzberg, F.; Kanovei, V.; Katz, K.; Katz, M.; Nowik, T.; Sherry, D.; Shnider, S. "Fermat, Leibniz, Euler, and the gang: The true history of the concepts of limit and shadow." Notices of the American Mathematical Society 61 (2014), no. 8, 848-864. https://www.ams.org/notices/201408/rnoti-p848.pdf, https://arxiv.org/abs/1407.0233. cited by over 50 articles:
14b. Katz, K.; Katz, M.; Kudryk, T. "Toward a clarity of the extreme value theorem." Logica Universalis 8 (2014), no. 2, 193-214. https://doi.org/10.1007/s11787-014-0102-8 and https://arxiv.org/abs/1404.5658 and https://www.ams.org/mathscinet-getitem?mr=3210286
14c. Sherry, D.; Katz, M. "Infinitesimals, imaginaries, ideals, and fictions." Studia Leibnitiana 44 (2012), no. 2, 166-192. https://www.jstor.org/stable/43695539, https://arxiv.org/abs/1304.2137 (Article was published in 2014 even though the journal issue lists the year as 2012) cited by over 50 articles:
14d. Tall, D.; Katz, M. "A cognitive analysis of Cauchy's conceptions of function, continuity, limit, and infinitesimal, with implications for teaching the calculus." Educational Studies in Mathematics 86 (2014), no. 1, 97-124. https://doi.org/10.1007/s10649-014-9531-9 and https://arxiv.org/abs/1401.1468
year '13 (8 publications)
13a. Bair, J.; Błaszczyk, P.; Ely, R.; Henry, V.; Kanovei, V.; Katz, K.; Katz, M.; Kutateladze, S.; McGaffey, T.; Schaps, D.; Sherry, D.; Shnider, S. "Is mathematical history written by the victors?" Notices of the American Mathematical Society 60 (2013) no. 7, 886-904. Accessible here, https://www.ams.org/notices/201307/rnoti-p886.pdf, https://www.ams.org/mathscinet-getitem?mr=3086638, https://arxiv.org/abs/1306.5973. cited by over 50 articles:
13b. Błaszczyk, P.; Katz, M.; Sherry, D. "Ten misconceptions from the history of analysis and their debunking." Foundations of Science 18 (2013), no. 1, 43-74. https://doi.org/10.1007/s10699-012-9285-8, https://www.ams.org/mathscinet-getitem?mr=3031794, https://arxiv.org/abs/1202.4153, and Reception. cited by 70 articles:
13c. Kanovei, V.; Katz, M.; Mormann, T. "Tools, objects, and chimeras: Connes on the role of hyperreals in mathematics." Foundations of Science 18 (2013), no. 2, 259-296. https://doi.org/10.1007/s10699-012-9316-5, https://arxiv.org/abs/1211.0244, https://www.ams.org/mathscinet-getitem?mr=3064607. cited by over 40 articles: Here we examine Alain Connes' criticisms of Robinson's framework.
13d. Katz, M.; Leichtnam, E. "Commuting and noncommuting infinitesimals." American Mathematical Monthly 120 (2013), no. 7, 631-641. https://doi.org/10.4169/amer.math.monthly.120.07.631, https://arxiv.org/abs/1304.0583, https://www.ams.org/mathscinet-getitem?mr=3096469. Here we examine Alain Connes' criticisms of Robinson's framework. cited by over 30 articles:
13e. Katz, M.; Schaps, D.; Shnider, S. "Almost equal: The method of adequality from Diophantus to Fermat and beyond." Perspectives on Science 21 (2013), no. 3, 283-324. https://doi.org/10.1162/POSC_a_00101, https://arxiv.org/abs/1210.7750, https://www.ams.org/mathscinet-getitem?mr=3114421. cited by 50 articles: Here we refute Herbert Breger's interpretation of Fermat and propose a sounder alternative.
13f. Katz, M.; Sherry, D. "Leibniz's infinitesimals: Their fictionality, their modern implementations, and their foes from Berkeley to Russell and beyond." Erkenntnis 78 (2013), no. 3, 571-625. https://doi.org/10.1007/s10670-012-9370-y, https://arxiv.org/abs/1205.0174, and https://www.ams.org/mathscinet-getitem?mr=3053644, cited by over 120 articles:
13g. Katz, M.; Tall, D. "A Cauchy-Dirac delta function." Foundations of Science 18 (2013), no. 1, 107-123. https://doi.org/10.1007/s10699-012-9289-4, https://arxiv.org/abs/1206.0119, and https://www.ams.org/mathscinet-getitem?mr=3031797
13h. Mormann, T.; Katz, M. "Infinitesimals as an issue of neo-Kantian philosophy of science." HOPOS: The Journal of the International Society for the History of Philosophy of Science 3 (2013), no. 2, 236-280. https://doi.org/10.1086/671348 and https://arxiv.org/abs/1304.1027, cited by over 50 articles:
year '12 (6 publications)
12a. Borovik, A.; Jin, R.; Katz, M. "An integer construction of infinitesimals: Toward a theory of Eudoxus hyperreals." Notre Dame Journal of Formal Logic 53 (2012), no. 4, 557-570. https://arxiv.org/abs/1210.7475, https://doi.org/10.1215/00294527-1722755, and https://www.ams.org/mathscinet-getitem?mr=2995420
12b. Borovik, A.; Katz, M. "Who gave you the Cauchy-Weierstrass tale? The dual history of rigorous calculus." Foundations of Science 17 (2012), no. 3, 245-276. https://doi.org/10.1007/s10699-011-9235-x, https://arxiv.org/abs/1108.2885, and https://www.ams.org/mathscinet-getitem?mr=2950620, as well as https://u.math.biu.ac.il/~katzmik/straw.html Here we examine Judith Grabiner's flawed Cauchy scholarship and propose a sounder alternative. cited by over 80 articles:
12c. Katz, K.; Katz, M. "Stevin numbers and reality." Foundations of Science 17 (2012), no. 2, 109-123. https://doi.org/10.1007/s10699-011-9228-9 and https://arxiv.org/abs/1107.3688 and https://www.ams.org/mathscinet-getitem?mr=2935194, cited by over 40 articles:
12d. Katz, K.; Katz, M. "A Burgessian critique of nominalistic tendencies in contemporary mathematics and its historiography." Foundations of Science 17 (2012), no. 1, 51-89. https://doi.org/10.1007/s10699-011-9223-1, https://arxiv.org/abs/1104.0375, and https://www.ams.org/mathscinet-getitem?mr=2896999 cited by over 40 articles:
12e. Katz, M.; Sherry, D. "Leibniz's laws of continuity and homogeneity." Notices of the American Mathematical Society 59 (2012), no. 11, 1550-1558. https://doi.org/10.1090/noti921, https://arxiv.org/abs/1211.7188, https://www.ams.org/mathscinet-getitem?mr=3027109, and https://u.math.biu.ac.il/~katzmik/straw2.html. cited by over 60 articles:
12f. Katz, M.; Tall, D. "Tension between intuitive infinitesimals and formal mathematical analysis." Chapter in: Bharath Sriraman, Editor. Crossroads in the History of Mathematics and Mathematics Education. The Montana Mathematics Enthusiast Monographs in Mathematics Education 12, Information Age Publishing, Charlotte, NC, 2012, pp. 71-89. https://arxiv.org/abs/1110.5747
year '11 (2 publications)
11a. Katz, K.; Katz, M. "Meaning in classical mathematics: Is it at odds with Intuitionism?" Intellectica 56 (2011), no. 2, 223-302. https://arxiv.org/abs/1110.5456, https://www.persee.fr/doc/intel_0769-4113_2011_num_56_2_1154 Here we examine Errett Bishop's criticisms of Robinson's framework. We also compare Bishop's attitude with Heyting's. Cited by over 30 articles:
11b. Katz, K.; Katz, M. "Cauchy's continuum." Perspectives on Science 19 (2011), no. 4, 426-452. https://doi.org/10.1162/POSC_a_00047, https://arxiv.org/abs/1108.4201, https://www.ams.org/mathscinet-getitem?mr=2884218. cited by 40 articles:
year '10 (3 publications)
10a. Ely, R. "Nonstandard student conceptions about infinitesimal and infinite numbers." Journal for Research in Mathematics Education 41 (2010), no. 2, 117-146.
10b. Katz, K.; Katz, M. "Zooming in on infinitesimal 1-.9.. in a post-triumvirate era." Educational Studies in Mathematics 74 (2010), no. 3, 259-273. https://doi.org/10.1007/s10649-010-9239-4 and
10c. Katz, K.; Katz, M. "When is .999... less than 1?" The Montana Mathematics Enthusiast 7 (2010), No. 1, 3-30.
List of 35 periodicals where the articles have appeared, in alphabetical order:
1. American Mathematical Monthly 13d
| Pioneer | Journal where reappraisal appeared | Link to article containing reappraisal | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Simon Stevin | Foundations of Science | 12c | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Bonaventura Cavalieri | Science in Context | 23g | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pierre Fermat | Perspectives on Science | 13e | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pierre Fermat | Foundations of Science | 18d | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pierre Fermat | Journal of Humanistic Mathematics | 20e | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pierre Fermat | Dedicated page | Fermat dedicated page | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| James Gregory | Foundations of Science | 18f | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| James Gregory | The Best Writings on Mathematics 2019, M. Pitici, Ed. | 19b | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Gottfried Leibniz | Notices AMS | 12e | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Gottfried Leibniz | Erkenntnis | 13f | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Gottfried Leibniz | Studia Leibnitiana | 14c | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Gottfried Leibniz | HOPOS (Journal of the International Society for the History of Philosophy of Science) | 16a | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Gottfried Leibniz | Mat. Stud. | 18a | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Gottfried Leibniz | British Journal for the History of
Mathematics| 21a |
Gottfried Leibniz | Antiquitates
Mathematicae | 21g |
Gottfried Leibniz | The Mathematical Intelligencer | 22b |
Gottfried Leibniz | Review of Symbolic
Logic | 24d |
Gottfried Leibniz | Dedicated page | Leibniz Dedicated page |
Leonhard Euler | The Mathematical Intelligencer |
15b |
Leonhard Euler | Journal for General Philosophy of
Science | 17b |
Leonhard Euler |
Dedicated page |
Euler's infinitesimal analysis |
A. L. Cauchy | Perspectives on Science | 11b |
A. L. Cauchy | Foundations of Science | 12b |
A. L. Cauchy | Foundations of Science | 13g |
A. L. Cauchy | Mat. Stud. | 17a |
A. L. Cauchy | Foundations of Science | 17e |
A. L. Cauchy | Foundations of Science | 18e |
A. L. Cauchy | Antiquitates Mathematicae | 19a |
A. L. Cauchy | Real Analysis Exchange | 20b |
A. L. Cauchy | British Journal for the History of
Mathematics | 20a |
A. L. Cauchy | Mathematics
Today | 21f |
A. L. Cauchy |
Dedicated page |
Cauchy's infinitesimal analysis |
Felix Klein |
Dedicated page |
Felix Klein |
Giuseppe Peano |
Dedicated page |
Giuseppe Peano |
Thoralf Skolem |
Dedicated page |
Thoralf Skolem |
|
List of critics in alphabetical order:
| Critic | Venue where rebuttal appeared | Link to article/venue containing rebuttal |
| Tom Archibald | Antiquitates Mathematicae | 22a, Section 5. See also Depictions |
| Richard Arthur | Erkenntnis | 13f |
| Richard Arthur | Foundations of Science | 17d |
| Richard Arthur | British Journal for the History of Mathematics | 21a See also Depictions |
| Richard Arthur | Ganita Bharati | 23f |
| Errett Bishop | Intellectica | 11a |
| Errett Bishop | Foundations of Science | 15a |
| Errett Bishop | Historia Mathematica | 18j |
| Bishop-Connes | Synthese | 17i |
| Errett Bishop | Dedicated page | Dedicated page |
| Umberto Bottazzini | Math Overflow | Q&A thread |
| Herbert Breger | Perspectives on Science | 13e |
| Herbert Breger | Foundations of Science | 18d |
| Rudopf Carnap | British Journal for the History of Mathematics | 21a, Section 1.7 |
| Alain Connes | Foundations of Science | 13c |
| Alain Connes | American Mathematical Monthly | 13d |
| Alain Connes | Math Overflow | Q&A thread |
| Alain Connes | Annals of Pure and Applied Logic | 21e |
| Alain Connes | Dedicated page | Dedicated page |
| John Earman | Erkenntnis | 13f |
| Kenny Easwaran | Notices of the American Mathematical Society | 14a |
| Kenny Easwaran | Mat. Stud. | 19d |
| Harold M. Edwards | Mathematical Intelligencer | 15b |
| Harold M. Edwards | Journal for General Philosophy of Science | 17b, section 4.13 |
| R. Erhardt | Journal for General Philosophy of Science | 26c |
| Giovanni Ferraro | Journal for General Philosophy of Science | 17b |
| Giovanni Ferraro | Foundations of Science | 18f. See also Depictions |
| Craig Fraser | Foundations of Science | 18e |
| Craig Fraser | Mat. Stud. | 17a, Section 4 |
| Craig Fraser | Math Overflow | Q&A thread |
| Haim Gaifman | Journal for General Philosophy of Science | 26c |
| C. Gilain | Antiquitates Mathematicae | 19a |
| Judith Grabiner | Foundations of Science | 12b |
| Judith Grabiner | Foundations of Science | 18e |
| Jeremy Gray | Foundations of Science | 17d. See also Depictions |
| Jeremy Gray | Stack Exchange | Q&A thread |
| Paul Halmos | Logica Universalis | 16b |
| Hide Ishiguro | Studia Leibnitiana | 14c |
| Hide Ishiguro | HOPOS (Journal of the International Society for the History of Philosophy of Science) | 16a |
| Douglas Jesseph | Antiquitates Mathematicae | 22a, Section 5. See also Depictions |
| Jesper Lützen | Mat. Stud. | 17a, Section 3. See also Depictions |
| Karl Marx | HOPOS | 26b |
| Ohad Nachtomy | Mat. Stud. | 18a, Section 1.7 |
| Marco Panza | Journal for General Philosophy of Science | 17b, Section 2.8, pp. 204-205. See also Depictions |
| Matthew W. Parker | Antiquitates Mathematicae | 24a |
| Alexander Pruss | Philosophia Mathematica | 21b |
| Alexander Pruss | Philosophia Mathematica | 21c |
| Alexander Pruss | Antiquitates Mathematicae | 24a |
| David Rabouin | Mat. Stud. | 18a, Sections 4.4, 4.6 |
| David Rabouin | British Journal for the History of Mathematics | 21a See also Depictions |
| Daviv Rabouin | Ganita Bharati | 23f |
| Gert Schubring | Foundations of Science | 17e See also Reception |
| Yaroslav Sergeyev | Foundations of Science | 17g |
| Yaroslav Sergeyev | EMS Surveys in Mathematical Sciences | "Both [EICs] have assumed responsibility for [the mistake of publishing Sergeyev's paper] and resigned from their position." |
| Yaroslav Sergeyev | Retraction Watch | Editors-in-chief of math journal resign over controversial paper |
| Yaroslav Sergeyev | Zentralblatt | Review by Louis Kauffman |
| Yaroslav Sergeyev | Mathematical Reviews | Review by Mikhail Katz |
| Yaroslav Sergeyev | dedicated page | Dedicated page |
| Reinhard Siegmund-Schultze | Antiquitates Mathematicae | 19a |
| Detlef Spalt | Perspectives on Science | 11b |
| Detlef Spalt | Antiquitates Mathematicae | 22a, Sections 3.2, 3.3 |
| Henry Towsner | Mat. Stud. | 19d |
| Klaus Viertel | Foundations of Science | 18e, Section 4.5 |
| Other critics of infinitesimals and/or Robinson | Journal where rebuttal appeared | Link to article containing rebuttal |
| Michel Rolle (1652-1719) | Mat. Stud. | 18a |
| George Berkeley (1685-1753) | Erkenntnis | 13f |
| George Berkeley (1685-1753) | Dedicated page | |
| François-Napoléon-Marie Moigno (1804-1884) | Erkenntnis | 13f |
| Georg Cantor (1845-1918) | Erkenntnis | 13f |
| Georg Cantor (1845-1918) | British Journal for the History of Mathematics | 25a, Section 3 |
| Bertrand Russell (1872-1970) | Erkenntnis | 13f, section 11.1 |
| Henk Bos (1940-2024) | Erkenntnis | 13f, section 11.3 |
| Henk Bos (1940-2024) | Journal for General Philosophy of Science | 17b, section 2.7 |
Videos
Where to start
Formalism versus Platonism
Non-Archimedean probabilities
Alok Singh's talk on NSA
Nonstandard analysis-based software
development
Introduction to infinitesimal analysis without the
axiom of choice (SPOT and SCOT)
Kathleen Sullivan's '76 study of teaching
calculus with infinitesimals based on Keisler's book
Amos Shalit:
An
analysis of Halmos's critique of nonstandard analysis
Arithmetic, Geometry, and Topology (AGT) Seminar:
current schedule
Jim
Holt, "Infinitesimally yours"
ABC's of infinitesimals
Special session AMS/IMU (Israel Mathematical
Union) on the history and philosophy of mathematics
Stevin
Cavalieri
Fermat
Leibniz
Berkeley
Euler
Cauchy
Riemann
Cantor
Klein
Peano
Skolem
Heyting
Robinson
Laugwitz
Nelson
Atiyah
Hrbacek
Keisler
Kutateladze
Kanovei
Teaching True Infinitesimal Calculus
Terry
Tao on ultrafilters, nonstandard analysis, and epsilon management
(june '07)
Terry
Tao on a cheap version of nonstandard analysis
Terry Tao: there is more to mathematics than rigor and proofs
Cauchy's sum theorem
Hyperreals and surreals