מבחן מחשבים מועד א' תשע"ה

שאלה 1

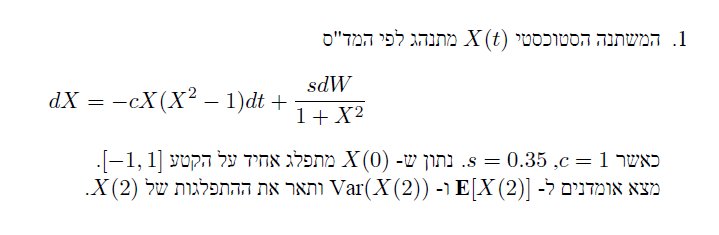
הנה הקוד שכתבתי לפתור:

c = 1;
s = 0.35; 
T = 2;
M = 10000;
N = 20; 
X = ones(M,N);
X(:,1) = -1 + 2*rand(M,1); 
Z = randn(M,N); 
h = T/N; 

for i=1:N
    X(:,i+1) = X(:,i)- h*c* X(:,i).*(X(:,i).^2-1) + sqrt(h)*s*Z(:,i)./(1+X(:,i).^2) ; 
end

hist(X(:,N+1),50)
mean(X(:,N+1))
var(X(:,N+1))

תוצאות: בארבע הרצות קבלתי את המספרים הבאים לתוחלת:

 
 -0.0036
  0.0010
 -0.0047
 -0.0079 

ואת התוצאות הבאות לשונות

 
 0.8248
 0.8313 
 0.8285 
 0.8324

האומדן לתוחלת: משהו קרוב ל-0. הטעות הסטוכסטית במקרה זה היא סטיית התקן (בערך 1) חלקי 100 (שורש M) שהוא בערך 0.01. ולכן לא ניתן להגיד יותר מזה. לגבי השונות, לא למדנו איך לתת אומדן לשגיאה, אבל התוצאה הנכונה היא 0.832 עד לטעות מסדר גודל של 0.001 (זה מהרצות עם M יותר גדול). לגבי ההתפלגות קבלתי התפלגות בי-מודלית :

שאלה 2

הנה הקוד שכתבתי לפתור:

S0=1;
r=0.01;
sigma=0.2;        
T=1;
N=252;
h=T/N;
M=10000;
S=S0*ones(M,N);
Z=randn(M,N);
K=[0.8:0.002:1.2];
aa=zeros(size(K));
for i=1:N
    S(:,i+1)=S(:,i).*exp((r-sigma^2/2)*h+sigma*sqrt(h)*Z(:,i));
end 
y1 = max(S,[],2);
y2 = min(S,[],2);
for i=1:length(K)
   opt1 = exp(-r*T)*(y1-K(i)).*(y1>K(i));
   opt2 = exp(-r*T)*(K(i)-y2).*(y2<K(i));
   aa(i)=corr(opt1,opt2);
end 
plot(K,aa)

תוצאה:

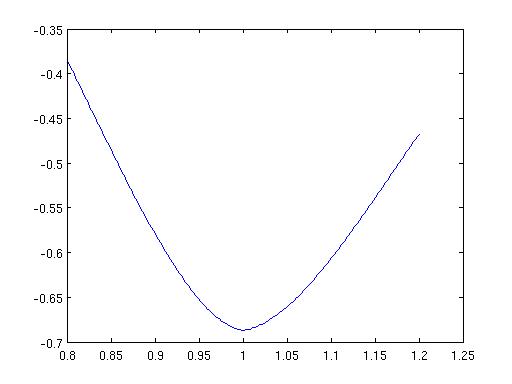
הסבר: האופציה הראשונה משלמת הרבה כאשר המחיר המקסימלי גבוה, השנייה כאשר המחיר המינימלי נמוך. בגדול יש קורלציה שלילית אבל לא מוחלטת - כי ייתכן מצב שבו גם המקסימום גבוה וגם המינימום נמוך, למרות שברוב הקרים עליה באחד גוררת עליה בשני. כל זה נכון כאשר K=1 שבו ניתן להיות בטוח ששתי האופציות ישלמו איזשהי תמורה. אבל אם, לדוגמה, K=0.9 יהיו מקרים שבהם המינימום הוא מעל זה והתמורה מאופציית ה-"מינימום" היא 0, שלא עולה עד המינימום יורד ל- K. וזה מחליש את הקורלציה השלילית.

שאלה 3

הנה הקוד שכתבתי לפתור: זו פונקציה המקבלת בקלט את מספר הצעדים ב-x ומספר הצעדים ב-t.

function z = jq3(N,M)

close all
h=1/N;
x=(0:N)*h; 
k=1/M;
c=10; 

u = zeros(N+1,M+1); 
u(:,1) = x;
u(N+1,:) = ones(1,M+1); 
plot(x,u(:,1))

for j=1:M
    u(2:N,j+1) = u(2:N,j) + k/h^2*(u(3:(N+1),j)-2*u(2:N,j)+u(1:(N-1),j)) - c*k*u(2:N,j).*(1-u(2:N,j));
end

plot(x,u(:,M+1)) 
z=u(1+N/2,M+1);

תוצאות:

jq3(10,200)   ->    0.27641 
jq3(20,800)   ->    0.27738 
jq3(40,3200)  ->    0.27763 

כאן רואים שעבור h=1/10 השתמשתי ב- k=1/200, עבור h=1/20 השתמשתי ב- k=1/800 ועבור h=1/40 השתמשתי ב- k=1/3200. אם משתמשים ב-k יותר גדול יש בעיית יציבות. הגרף נראה אותו דבר בכל מקרה:

Back to main course page
Back to my main teaching page
Back to my home page