
הנה הקוד שכתבתי לקבל תשובות לערך בודד של b:
function a=kq1(b)
N = 100;
M = 50000;
h = 2/N;
Z = randn(M,N);
X = ones(M,1);
for i=1:N
X = X + h*1.6*(1-X) + sqrt(h)*b*sqrt(abs(X)).*Z(:,i);
end
a = [b,mean(X), std(X)/sqrt(M), var(X)];
end
הנה תשובות מספריות :
b E[X(2)] error Var(X(2)) 0.1 0.9996 0.0003 0.0032 0.5 1.0016 0.0013 0.0801 1.0 1.0032 0.0025 0.3200 2.0 1.0023 0.0051 1.2869 5.0 1.0030 0.0179 16.0398
רואים שכאשר b עולה הערך של התוחלת בקושי משתנה - נשאר קבוע (שווה 1) עד לדיוק של סימולציות שלנו. מאידך, הושנות עולה מהר עם b. וזה לא מפתיע - b מכפיל את האיבר הסטוכסטי במשוואה וגורם ליותר תנודתיות.

הנה הקוד שכתבתי לפתור לערכים בודדים של B ו- rho.
function a=kq2(rho,B)
S10=1;
S20=1;
r=0.02;
sigma1=0.15;
sigma2=0.08;
K=1.1;
N=252;
M=50000;
T=1;
h=T/N;
Z1=randn(M,N);
Z2=randn(M,N);
S1=S10*ones(M,N+1);
S2=S20*ones(M,N+1);
for i=1:N
S1(:,i+1)=S1(:,i).*exp( (r-sigma1^2/2)*h + sigma1*sqrt(h)*Z1(:,i) );
S2(:,i+1)=S2(:,i).*exp( (r-sigma2^2/2)*h + sigma2*sqrt(h)*(rho*Z1(:,i)+sqrt(1-rho^2)*Z2(:,i)) );
end
P = exp(-r*T) * (S1(:,end)-K) .* (S1(:,end)>K) .* (min(S2,[],2)>B);
a=[ rho, B, mean(P), std(P)/sqrt(M) ];
כאשר הפעלתי עם rho=0.4 ו- B=0.9 קבלתי תוצאה 0.0150 עם טעות סטוכסטית 0.0002. הערך הוא סביר - אין הרבה סיכוי שהנכס הראשון יהיה מעל 1.1 בסוף.
קורלציה יותר גבוהה מורידה את האפשרות שהנכס הראשון יהיה מעל ל-K אבל האופציה תפסל בגלל שהנכס השני ירד מתחת למחסום. ואכן כאשר rho=0.6 מקבלים תוצאה 0.0182 עם טעות סטוכסטית 0.0003 וכאשר rho = 0.2 מקבלים תוצאה 0.0119 עם טעות סטוכסטית 0.0002.
מאידך כאשר B עולה, יש יותר הסתברות שהאופציה תפסל. מקבלים תוצאות כדלהלן:
B value error 0.85 0.0203 0.0003 0.90 0.0152 0.0002 0.95 0.0089 0.0002
כמובן אפשר לפרט הרבה יותר מזה ....

הנה קוד שכתבתי לפתור את הבעיה ולצייר את u(x,t) כפונקציה של x לערכים השונים של t:
N = 20;
M = 1000;
x = (0:N)/N;
t = (0:M)/M;
h = 1/N;
k = 1/M;
u = zeros(N+1,M+1);
u(N+1,:) = sin(20*t');
for i=1:M
u(2:N,i+1) = u(2:N,i) + k/h^2*( u(3:(N+1),i) - 2*u(2:N,i) + u(1:(N-1),i ));
plot(x,u(:,i))
axis([0 1 -1 1])
drawnow
end
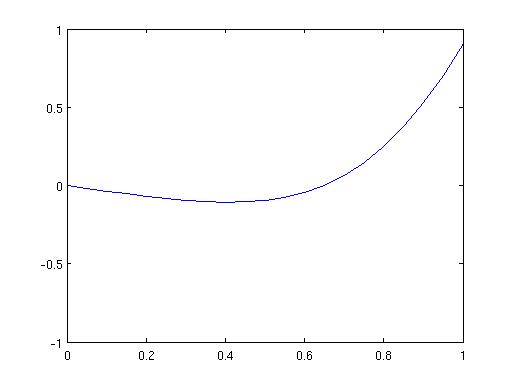
הנה הפתרון בזמן
t=1:

אפשר להגדיל ולראות שיש שורש בין 0.635 ו-0.655. כדי לשפר את הדיוק כדאי להריץ שוב עם N=100 ו- M=25000 (ה- M נבחר לשמור על יציבות). הגרף מאוד דומה. על ידי הגדלת הגרף ניתן לראות שורש די קרוב ל- x=0.64 . וגם נקודוה קריטית (מינימום) איפה שנגזרת היא 0 ב- x=0.40 . ניתן - ואולי מומלץ - לוודא תשובות אלה על ידי שמסתכלים לא רק על הגרף, אלא גם על הערכים שמתקבלים בסוף.
Back to main course page
Back to my main teaching page
Back to my home page