מבחן מחשבים מועד א' תשע"ו

שאלה 1

הקוד שאני כתבתי להפעיל שיטת אויילר על המד"ס ולחשב את ההסתברות:

a = 0:0.1:2; 
b = 0.02 ;   
c = 0.04 ; 
r0 = 0.03 ;

M = 10000;
N = 100;
h = 1/N; 
Z = randn(M,N);
an = zeros(size(a)); 

for i=1:length(a)
   r = r0 * ones(M,N+1);
   for j=1:N
       r(:,j+1) = r(:,j) + a(i)*(c-r(:,j))*h + b*sqrt(h)*Z(:,j);
   end
   an(i)=sum(min(r,[],2)<0)/M;
end

figure(1)
plot(a,an)
figure(2)
plot(a,sqrt(an.*(1-an)/M))

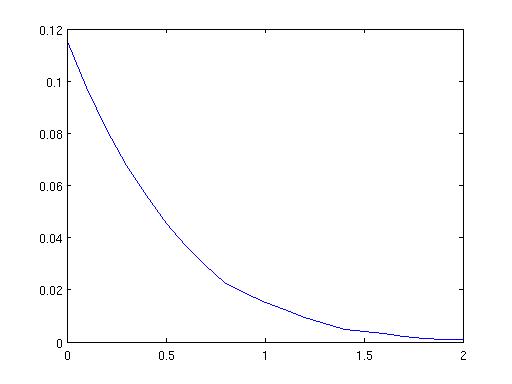
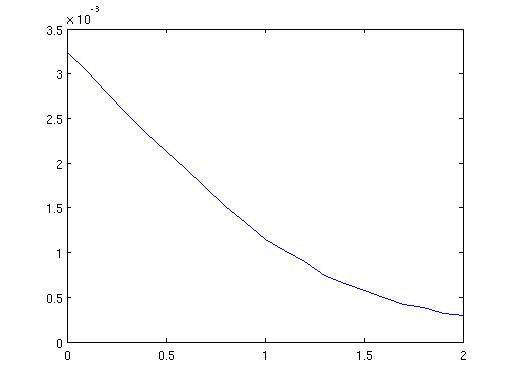
הגרפים - צד ימין האומדן להסתברות, צד שמאל הטעות הסטכסטית

הערכים כאשר a=0.1 יוצאים כך: הסתברות 0.0134, טעות סטוכסטית 0.0011. יחסית להסתברות הטעות היא די גבוהה. אפשר להוריד על ידי שימוש ב-M יותר גדול.

שאלה 2

יש כמה וכמה אפשרויות בשאלה זו. האופציות על כל נכס ונכס בנפרד הן אופציות סטנדרטיות וניתן להשתמש בנוסחת בלק-שולס לתמחר אותן (גם יש להעיר שהמחירים של אופציות אלו אינם תלויים על מקדם המתאם rho ). לאופציה על הסכום אין נוסחה ויש צורך לעשות סימולציה. ולכן - בגלל העקרון של משתנים מקריים משותפים - זה דווקא לא רעיון רע להשתמש באותה סימולציה גם למחירים של האופציות הפשוטות. הקוד שלי מקבל כקלט את הערכים של K ושל rho ומחזיר את ההפרש של ערך האופציה על הזוג וסכום הערכים של שתי האופציות על נכסים בודדים:

function an = q2(K,rho)

r = 0.02; 
sig1 = 0.1;
sig2 = 0.2;
S10 = 10;
S20 = 20;
K1 = 11;
K2 = 22; 
T = 1; 

M = 50000;
Z1 = randn(M,1);
Z2 = randn(M,1); 

S1 = S10*exp( (r-sig1^2/2)*T + sig1*Z1*sqrt(T) ); 
S2 = S20*exp( (r-sig2^2/2)*T + sig2*(rho*Z1+sqrt(1-rho^2)*Z2)*sqrt(T) ); 
.
o1 = (S1-K1).*(S1>K1);
o2 = (S2-K2).*(S2>K2);
o3 = (S1+S2-K).*(S1+S2>K);
p = o3-o1-o2;

an = [mean(p), std(p)/sqrt(M)];

מתחילים לשחק עם זה:

q2(31,-0.5)  ->  0.1496    0.0031
q2(31,-0.7)  ->  0.0600    0.0029
q2(31,-0.9)  ->  -0.0363    0.0025

רואים שההפרש יורד כפונקציה של rho.עוד תוצאות:

q2(31,-0.81)  ->   0.0073    0.0027
q2(31,-0.82)  ->  -0.0024    0.0027
q2(31,-0.83)  ->  -0.0007    0.0027
q2(31,-0.84)  ->  -0.0113    0.0026

אני די משוכנע שהתשובה היא בין 0.84 - ל- 0.81 - התשובה שלי לשאלה הראושנה: 0.825 - פלוס מינוס 0.015

כמו כן לשאלה השנייה:

q2(32.46,0.5)  -> -0.0085    0.0016
q2(32.45,0.5)  -> -0.0020    0.0016
q2(32.44,0.5)  -> -0.0007    0.0016
q2(32.43,0.5)  ->  0.0045    0.0016
q2(32.42,0.5)  ->  0.0067    0.0016

התשובה שלי לשאלה השנייה: 32.44 פלוס מינוס 0.02

שאלה 3

הקוד הבסיסי שלי לפתור= עם שיטת אויילר:

function a=q3(M)

N = 20; 
h = 4/N; 
k = 1/M; 
x = -2 + 4*(0:N)/N;
t = 1*(0:M)/M;

u = x+2;
for i = 1:M
    u(2:N) = u(2:N) + k/h^2*( u(3:(N+1)) - 2*u(2:N) + u(1:(N-1)) )- k*u(2:N); 
    u(N+1) = u(N) + h;
end

plot(x,u)
a = u(N+1);

כאשר מפעילים עם N=20 - אפשר M=46 פחות מזה לא כל כך ברור. אם אני משנה ל- N=40 אזי המינימום הוא M=195 ואם N=80 המינימום הוא M=794. כל פעם שאני מעלה את N ב-2 יש צורך להעלות את M ב-4.

כאשר הסתכלתי על הערכים של u שיצאו - לכל N העליתי את M עד שאין עוד שינוי ומצאתי את הערכים הבאים (שבפורמט short מבטיח את הדיוק הרצוי): עבור N=20 קבלתי 1.9665, עבור N=40 קבלתי 1.9317 , עבור N=80 קבלתי 1.9151 .

Back to main course page
Back to my main teaching page
Back to my home page