Exercise Set 5, Question 3

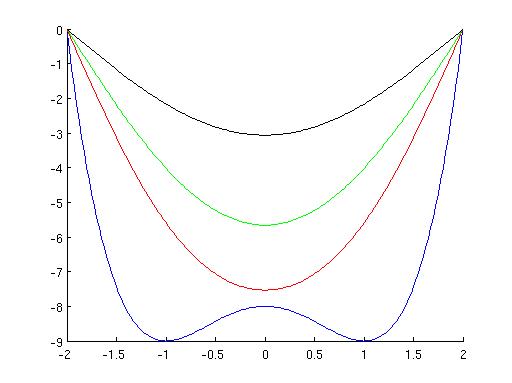
function t5q3(h,k)

% set up the grid
T = 2 ;
Xmin = -2 ;
Xmax = 2 ;
N = (Xmax-Xmin)/h ;    % assume this is an integer 
M = T/k ;              % assume this is an integer 
x = Xmin + (0:N)*h ; 
% t = (0:M)*k ;

% prepare matrix to hold the solution
u = zeros(M+1,N+1); 
% no need to impose boundary conditions as they are zero
u(1,:) = x.^4 - 2*x.^2 - 8 ;
% Euler method to evolve
for j=1:M 
   u(j+1,2:N) = u(j,2:N) + k/h^2*( u(j,3:(N+1)) - 2*u(j,2:N) + u(j,1:(N-1)) );  
end

% plot the solution at times 0, 0.5, 1, 2 
% color blue,red,green and black
figure(1)
hold on
plot(x,u(1,:),'b');
plot(x,u(M/4+1,:),'r');
plot(x,u(M/2+1,:),'g');
plot(x,u(M+1,:),'k');

For k=1/500 it only works for h=1/10, and not for h=1/20, h=1/40.
For k=1/1000 it works for h=1/10 and h=1/20, and not for h=1/40.
Also for k=1/2000 it works for h=1/10 and h=1/20, and not for h=1/40.
For k=1/4000 it works for h=1/10, h=1/20, and h=1/40.

This is a result of the STABILITY CONDITION k<h^2/2. For example for h=1/40, this condition says k<1/3200. You can check it does work for k=1/3300 but not for k=1/3100. This is the answer for question (a).

For question (b) - the error of the Euler method is supposed to behave as O(k) + O(h^2). Suppose we change the above program to return the approximate value of u(0,1), but changing the first line to

function v=t5q3(h,k)

and adding a line at the end

v=u(M/2+1,N/2+1); 

Here are results for h=1/10, and k=1/500,1/1000,1/2000,1/4000:

-5.66050
-5.66140
-5.66185
-5.66207

Using very small k (and h=1/10) gives a value of -5.66229. The above values deviate from this by

0.00179
0.00089
0.00044
0.00022

We see that WHEN WE HALVE k WE HALVE THE CONTRIBUTION TO THE ERROR - confirming that the error dependence on k is O(k).

Here, on the other hand are results for k=1/4000, and h=1/10,1/20,1/40:

-5.66207
-5.66096
-5.66068

We cannot reduce h more without violating the stability condition. But supposing that the value for very small h is -5.66059 (I won't explain how I got this) the errors are

0.00148
0.00037
0.00009

We see that WHEN WE HALVE h WE QUARTER THE CONTRIBUTION TO THE ERROR - confirming that the error dependence on h is O(h^2).

For question (c). Looking at the plot above we see that the function starts out with 2 minima and 1 maximum and then "relaxes" to zero, becoming a "unimodular function", with just a single minimum at zero. How can we find the minimum value of t for which the function is unimodular? Add the following lines in the j loop:

if ( u(j+1,N/2+1)-u(j+1,N/2) ) * ( u(j,N/2+1)-u(j,N/2) ) < 0 
   v=(j+1)*k;
end 

(and comment out the previous definition of v). This prints the new time (j+1)k if there is a change in the sign of the slope at x=0.

Running this with k=1/4000,h=1/40 gives the time unimodality is reached as 0.169. Running with k=/20000,h=1/100 gives 0.16885. The accuracy of these answers can be approved, but this is not for here.