Approximation by orthogonal projection 

We are going to  approximate the function v = sin(x) on the interval [0 , Pi/2]  

using the orthogonal set P0(z), P1(z), P2(z), P3(z),  where  z = 4x/Pi - 1  

(in general on the interval [a,b] use the Pn( (2x-a-b)/(b-a) )  

>

 

 

 

 

	(1)

 

Check these are orthogonal if you like.  

>

 

(2)

 

Compute the Fourier coefficients 

>

 

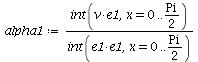(3)

 

>

 

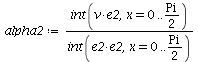(4)

 

>

 

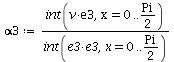(5)

 

>

 

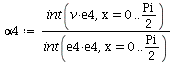(6)

 

Approximation using 3 basis functions:  

>

 

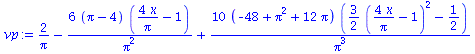(7)

 

>

 

(8)

 

>

 

>

 

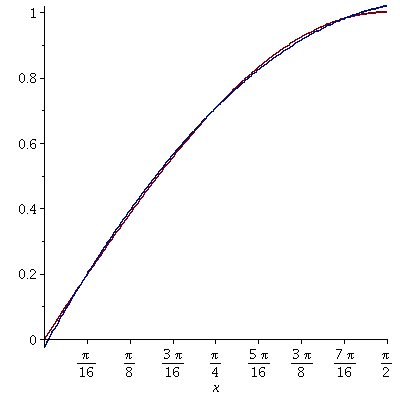(9)

 

Approximation using 4 basis functions  

>

 

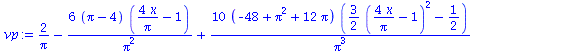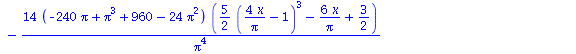(10)

 

>

 

(11)

 

>

 

>

 

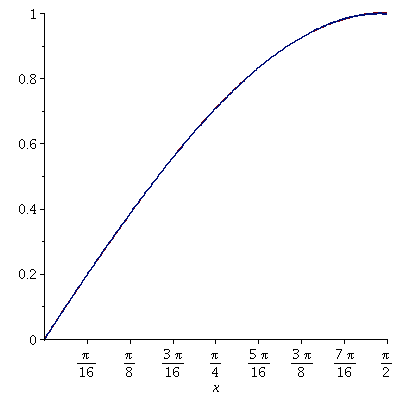(12)

 

>