Commuting Extensions of Matrices

Making matrices for commuting extension experiments in Maple

>	restart; with(LinearAlgebra):

Case 1: a pair of 6x6 matrices which are top left hand blocks of a pair of commuting 7x7's:

>	Z:=< <1,-1,0,0,0,1,0> | <-1,2,1,0,0,0,0> | <0,1,-1,2,0,0,0> | <0,0,1,2,1,0,0> | <0,0,0,1,1,-2,-1> | <1,0,0,0,-2,2,1> | <0,0,0,0,0,1,2>  >:

>	Q:=op(1,[QRDecomposition(Z)]):

>	D1:=DiagonalMatrix([1,2,3,4,-2,-3,4]):  D2:=DiagonalMatrix([-1,5,6,-4,1,-2,-2]):

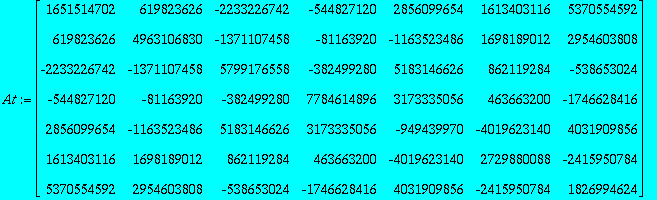
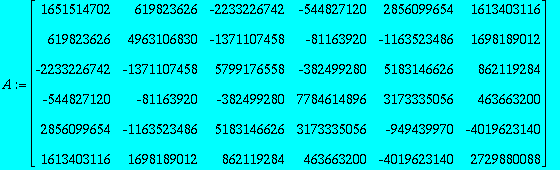
>	At:=2645094192*Q.D1.Transpose(Q); Bt:=2645094192*Q.D2.Transpose(Q);

Check commutator is zero:

>	At.Bt-Bt.At;

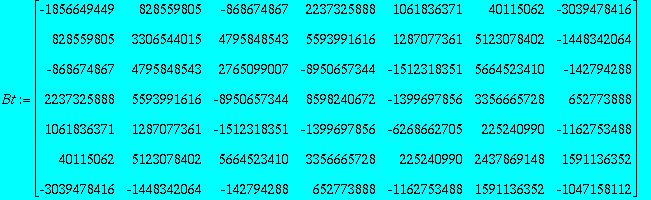
Make A,B

>	A:=SubMatrix(At,1..6,1..6); B:=SubMatrix(Bt,1..6,1..6);

Check rank of commutator

>	Rank(A.B-B.A);

Case 3: a pair of 6x6 matrices which are top left hand blocks of a pair of commuting 8x8's:

>	Z:=< <1,-1,0,0,0,1,0,0> | <-1,2,1,0,0,0,0,0> | <0,1,-1,2,0,0,0,1> | <0,0,1,2,1,0,0,0> | <0,0,0,1,1,-2,-1,0> | <1,0,0,0,-2,2,1,0> | <0,0,0,0,0,1,2,-1> |<0,0,0,0,0,1,1,-2> >:

>	Q:=op(1,[QRDecomposition(Z)]):

>	D1:=DiagonalMatrix([1,0,2,3,4,-2,-3,4]):D2:=DiagonalMatrix([-1,5,0,6,-4,1,-2,-2]):

>	At:=11948255340*Q.D1.Transpose(Q); Bt:=11948255340*Q.D2.Transpose(Q);

Check commutator is zero:

>	At.Bt-Bt.At;

Make A,B

>	A:=SubMatrix(At,1..6,1..6); B:=SubMatrix(Bt,1..6,1..6);

Check rank of commutator

>	Rank(A.B-B.A);

Case 4: a pair of 6x6 matrices which are top left hand blocks of a pair of commuting 9x9's:

>	Z:=< <1,-1,0,2,0,0,0,1,0> | <-1,2,1,0,0,0,0,0,0> | <0,1,-1,2,0,0,0,0,1> | <0,0,1,2,1,0,0,0,0> | <0,0,0,1,1,-2,-1,0,0> | <1,0,0,0,-2,2,1,0,0> | <0,0,0,0,0,1,2,-1,0> |<1,0,0,0,0,1,1,-2,-1> | <0,-1,0,0,0,0,0,1,1> >:

>	Q:=op(1,[QRDecomposition(Z)]):

>	D1:=DiagonalMatrix([0,1,-12,22,-101,33,-3,41,-4]):D2:=DiagonalMatrix([5,23,6,16,7,-7,-1,0,-2]):

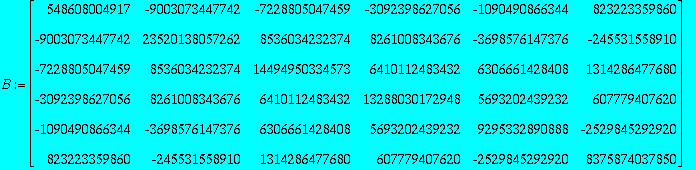
>	At:=1686774949860*Q.D1.Transpose(Q); Bt:=1686774949860*Q.D2.Transpose(Q);

Check commutator is zero:

>	At.Bt-Bt.At;

Make A,B

>	A:=SubMatrix(At,1..6,1..6); B:=SubMatrix(Bt,1..6,1..6);

Check rank of commutator

>	Rank(A.B-B.A);

Case 2: Making a one parameter family of pairs of matrices with rank 2 commutator  

>	a1:=Vector([1,-2,2,0,-1,3]): a2:=Vector([2,-1,0,2,1,2]): a3:=Vector([1,0,0,-1,-1,t]): a4:=Vector([1,-2,1,2,0,2]):

>	A:=Matrix(6,6): B:=Matrix(6,6): for i from 1 to 6 do A[i,i]:=a1[i]; B[i,i]:=a2[i]; end do:

>	for i from 1 to 6 do for j from 1 to 6 do if i<>j then B[i,j]:=A[i,j]+(a3[i]*a4[j]-a4[i]*a3[j])/(a1[i]-a1[j]) end if end do end do;

>	A:=6*A;B:=6*B;

check rank condition

>	Rank(A.B-B.A);

to see whether A,B have a 7x7 commuting extension we have to check whether a certain determinant vanishes:

>	d:=5*Determinant( < a1 | a2 | A.a1 | A.a2 | B.a1 | B.a2> )/128/81;

>

For most values of t this is non zero, for example can use t=1