Grain Growth
Cellular structures can be found in many natural systems, including biological tissue, soap foams, polycrystalline metals, and international borders. Almost all of these systems change with time. For example, if you watch the bubbles in your kitchen sink, you might notice that some grow while others shrink and disappear. Understanding how these systems evolve is crucial for understanding their long-time properties.
Two Dimensions
In the early 1950's John von Neumann proved that in two dimensional systems, bubbles with more than six neighbors grow, those with fewer shrink, and those with exactly six
neither grow nor shrink (though they can change shape).
More precisely, von Neumann showed that the area of each bubble changes as:
dA/dt = -2 π M γ (1 - n/6),where A is the area of the bubble, M and γ are constants describing the mobility and surface tension of the boundary, and n is its number of neighbors. This beautiful result is both elegant and remarkably simple. A few years later, Mullins extended this result to the case of two-dimensional grain growth structures with isotropic boundary energies. This result advanced the mathematical study of grain growth, a central topic in the study of polycrystalline materials.
Here is a twenty second simulation of the evolution of a two-dimensional network of 1000 grains. At every step, von Neumann's law is satisfied for each grain with error of order Δt^2; the system evolves until there remain only 165 grains.
Three Dimensions
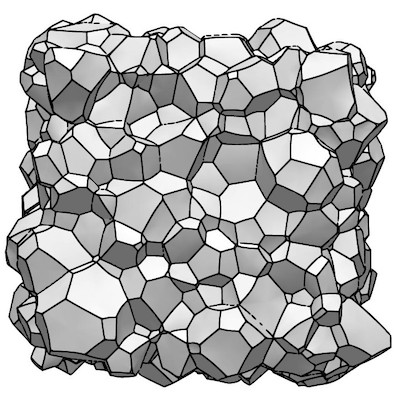
The story in higher dimensions becomes significantly more complicated. Unlike the rules in two dimensions, which are purely topological (a cell's growth depends only its number of neighbors), in three and higher dimensions the analogous rate of change depends on the cell's geometry.Here is a simulation of a three-dimensional system evolving over time. The system begins as Voronoi tessellation with 1000 grains and stops when roughly 50 grains remain. Here (alternatively here) we describe some of the shapes that arise in three-dimensional grain-growth structures. Those might be contrasted with those found in Poisson-Voronoi tessellations.
The above work was done jointly with David Srolovitz, Robert MacPherson, and Jeremy Mason.
Some ideas related to one-dimensional systems (see video below) can be found in my PhD thesis. Some recent exact results obtained with Robin Pemantle are reported here.
Other work was done with Aaron Koolyk, Benjamin Matschke, and Amanda Redlich.
Return to other research interests.