Voronoi Topology for Structure Analysis
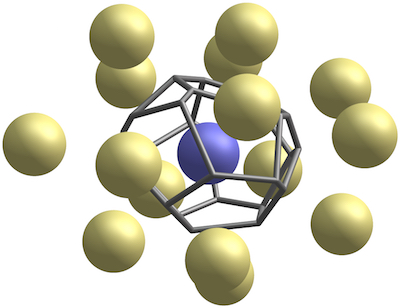A common challenge in studying many physical systems is describing the "structure" of a set of points in space. Group theory provides powerful tools to study perfectly ordered systems, and probability theory provides tools to study "perfectly disordered" systems. Real systems, however, tend to be neither perfectly ordered not perfectly disordered. A meaningful way to describe this structure, in an elegant and practical manner, motivates the development of the Voronoi topology method, implemented in VoroTop.
Statistics of Three-Dimensional Poisson-Voronoi Structures
Voronoi tessellations of Poisson point processes are widely used for modeling many physical and biological systems. In this paper (preprint), we analyze simulated Poisson-Voronoi structures containing a total of 250,000,000 cells to provide topological and geometrical statistics of this important class of networks. To date, this is the largest data set for this type of system (by at least two orders of magnitude); moreover, many topological features of this system have not been considered until now.Please be in touch with any questions; we are especially eager to provide additional statistics. Additional raw data for these structures is available here.
If you use this data in published work, please consider citing one of the papers below.
| Filename | Description |
|---|---|
| all_pvectors.data | Distribution of all 375,410 observed p-vectors |
| top_10000_wvectors.data | Distribution of 10,000 most common Weinberg vectors |
| edges_dist_areas_perims.data | Distribution of edges, and average area and perimeter |
| faces_dist_vols_areas.data | Distribution of faces, and average volume and surface area |
| p_vectors_and_types.data | Counts of possible and observed p-vectors and topological types |
| symmetries.data | Distribution of symmetry orders |
| areas_distribution.data | Distribution of areas of all faces |
| faces_areas_distributions.data | Distribution of areas of all faces with fixed number of edges |
| perims_distribution.data | Distribution of perimeters of all faces |
| faces_perim_distributions.data | Distribution of perimeters of all faces with fixed number of edges |
| volumes_distribution.data | Distribution of volumes of all cells |
| faces_volumes_distributions.data | Distribution of volumes of all cells with fixed number of faces |
| surface_areas_distribution.data | Distribution of surface areas of all cells |
| faces_surface_areas_distributions.data | Distribution of surface areas of all cells with fixed number of faces |
| weaire-aboav.data | Expected number of neighbors m(F) of cells with F faces |
| kentropy.data | k-entropy for 0 <= k <= 8 |
| vertices.data | Vertices, characterized by total faces of four neighbors (*) |
| face_round.data | Roundness of faces with n edges |
| cell_round.data | Roundness of cells with F faces |
Addition fun data
The 250,000,000 Poisson-Voronoi cells contained:- 325 tetrahedra,
- 23744 cubes,
- 3612 pentagonal dodecahedra, and
- 623 Kelvin cells.
-
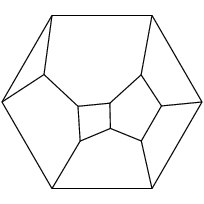The most frequently occuring polyhedron (686,096 occurances, or roughly 0.27% of all observed cells) has 1 triangular face, 3 quadrilateral faces, 3 pentagonal faces, and 2 hexagonal faces. A Schlegel diagram of this polyhedra appears to the right.
Random fun fact
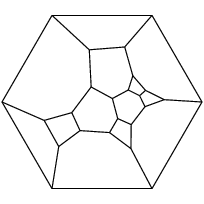
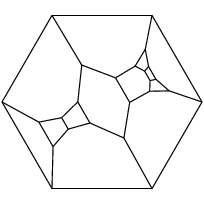
You might know that the `Kelvin cell', a very symmetric 14-faced polyhedron, has 6 quadrilateral faces and 8 hexagonal faces. Kelvin conjectured that this shape tiles three-dimensional space with a minimal surface area among all space-filling polyhedra. What you might not know is that the Kelvin cell is not the only polyhedron with this set of faces. Below are Schlegel diagrams of the Kelvin cell and of two other polyhedra with 6 quadrilateral faces and 8 hexagonal faces which are most certainly not the Kelvin cell; these are the only other such polyhedra.
Related Publications
- Lazar, E.A., Han, J. and Srolovitz, D.J. "A Topological Framework for Local Structure Analysis in Condensed Matter", arXiv, Proc. Natl. Acad. Sci. 112:E5769 (2015).
- Leipold, H., Lazar, E.A., Brakke, K.A., and Srolovitz, D.J. "Statistical Topology of Perturbed Two-Dimensional Lattices", arXiv, (accepted to J. Stat. Mech.).
- Lazar, E.A., Mason, J.K., MacPherson, R.D. and Srolovitz, D.J. "Statistical topology of three-dimensional Poisson-Voronoi cells and cell boundary networks", arXiv, Phys. Rev. E. 88:063309, 2013.
- Hilhorst, H.J., Lazar, E.A. "Many-faced cells and many-edged faces in 3D Poisson-Voronoi tessellations", arXiv, J. Stat. Mech. 10:P10021, 2014.
- Lazar, E.A., Mason, J.K., MacPherson, R.D. and Srolovitz, D.J. "Complete topology of cells, grains, and bubbles in three-dimensional microstructures", arXiv, Phys. Rev. Lett. 109:095505, 2012.