Schlegel Diagrams
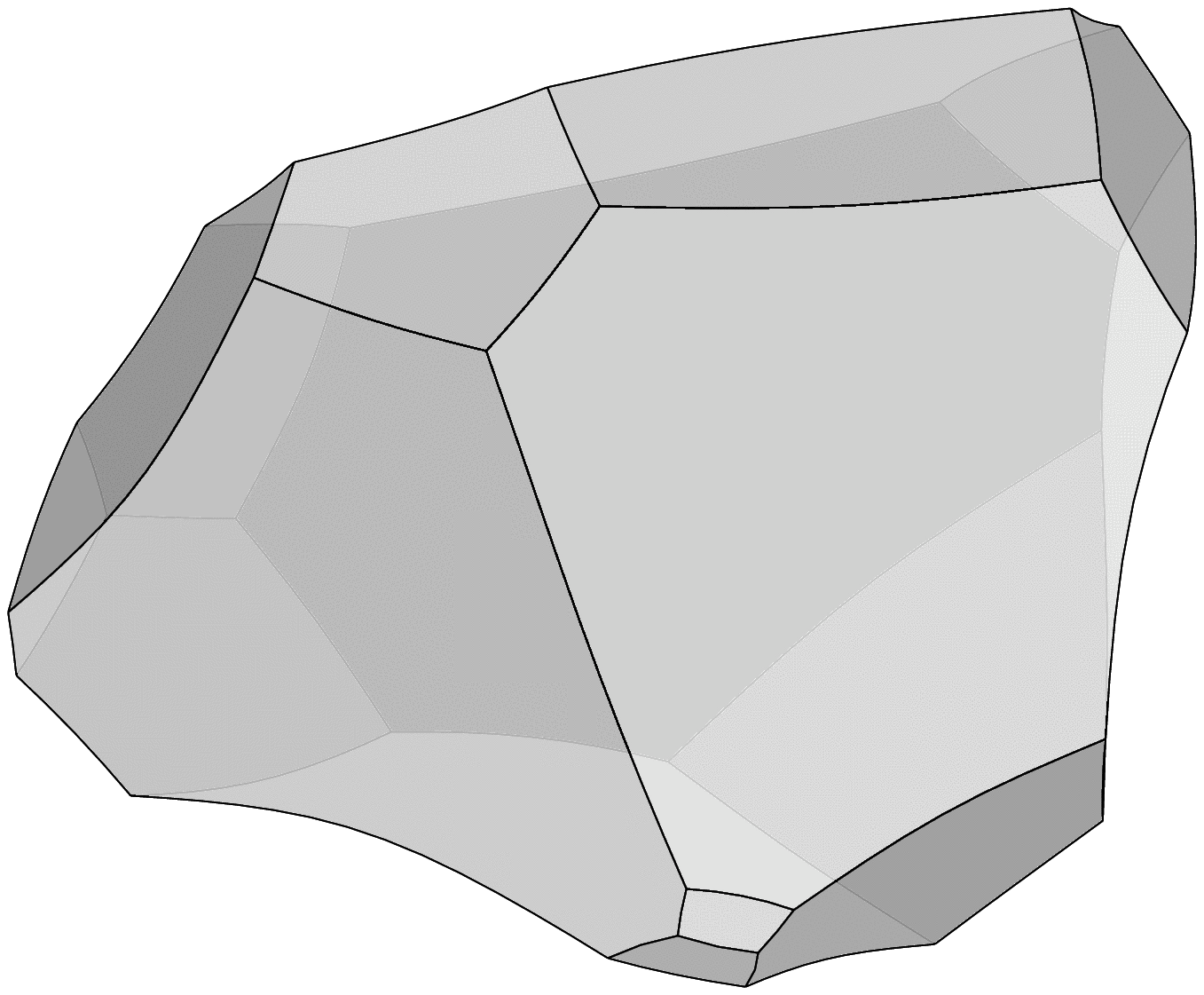 A Schlegel diagram is the projection of a polytope from d-dimensional space into d-1 dimensions. Schlegel diagrams can be useful for studying three-dimensional polyhedra. For example, we might project a three-dimensional cube onto the plane, as illustrated in the figure to the left.
A Schlegel diagram is the projection of a polytope from d-dimensional space into d-1 dimensions. Schlegel diagrams can be useful for studying three-dimensional polyhedra. For example, we might project a three-dimensional cube onto the plane, as illustrated in the figure to the left.
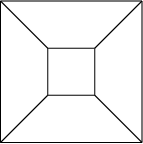 One face of the polyhedron is chosen to be the "outside" face. In the example on the left, one of the square faces is chosen as the outside face, and the remaining faces are projected inside that one. This allows us to "look" at the entire shape at once.
One face of the polyhedron is chosen to be the "outside" face. In the example on the left, one of the square faces is chosen as the outside face, and the remaining faces are projected inside that one. This allows us to "look" at the entire shape at once.
Algorithm
Schlegel diagrams can be made in the following manner. We first choose one face of the polyhedron; it is often convenient to choose one of the faces with a maximal number of edges. For example, if we were to draw the Schlegel diagram of a polyhedron with a hexagonal face and no faces with more than six edges, we then choose a hexagonal face as the outside face. We then take each of the vertices of the maximal outside face and spread them out evenly on the unit circle. Next, we place all remaining vertices at the origin. Meanwhile, we are careful to keep track of which vertices are connected to which other vertices through edges. We then repeat the following process: we move each vertex to the center of its (three) neighboring vertices, leaving the vertices on the boundary circle fixed. After a few iterations, we are left with a nice-look Schlegel diagram. All Schlegel diagrams on this website were constructed using this method.Symmetries
A word should be said about symmetries of polyhedra and the way in which they can be seen in Schlegel diagrams. At first glance, the Schlegel diagram of a shape highlights some of its many symmetries. For example, the diagrams below to the right appear very symmetric, and this reflects the natural symmetries of these shapes (the tetrahedron, the pentagonal dodecahedron, and the Kelvin truncated octahedron).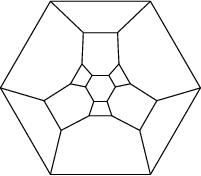
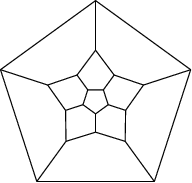
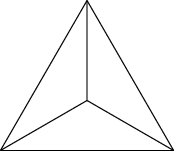
However, a Schlegel diagram can also obscure other symmetries. Of the three diagrams at the bottom of the page, the one in the middle might appear to be the least symmetric. However, of the three, the one in the middle actually has the symmetry group with the highest order (8, compared with 4 for the one on the left and 6 for the one on the right).
To understand this apparent oddity, it is worth pointing out that the diagrams on the left and right each have one maximal (hexagonal) face. Therefore, aside from rotations or reflections, there is no way to redraw identical graphs using a different face as the outside face. The middle diagram, in contrast, has four pentagonal faces, and it so happens that identical graphs can be drawn with each of those faces as the outside polygon. These contribute additional symmetries which might be initially overlooked when considering the Schlegel diagrams.
Click here for Schlegel diagrams of all convex, simple polytopes with 10 or fewer faces, and here for Schlegel diagrams of the 35 most common cell topologies in the Poisson--Voronoi microstructure.
Comments or questions? Want to see the Schlegel diagram of a specific shape? Feel free to drop me a line at mlazar @ math.biu.ac.il.
Return to other research interests.
